今回のテーマは三角形の種類です。前回は三角形の角度について学びましたが、ここではどのような種類の三角形があるのかについて学びます。
この記事はうちの子が3年生で学習した算数を振り返り、解説を備忘録的にまとめておこうというシリーズ。教え方は学校の先生、塾の先生、親など教える人それぞれだと思いますので、参考程度にみていただければと思います。
中学受験 は算数がキモといっても過言ではありません。論理的思考はどの教科を学ぶにおいても重要となる、鍛えておくべき力だと個人的には思っています。
問題・解答はPCで作図するより手書きが一番早いので、手書きでまとめています。少々見辛い箇所もあるかと思いますが、ご了承ください。
前回の記事はこちらから。
次の記事はこちらから。
覚える三角形は3つ
まずは3つの三角形を覚えます。そのうち、二つは筆箱の中に隠れていていつでも見ることができます。ひとつづつ特徴を見ていきましょう。
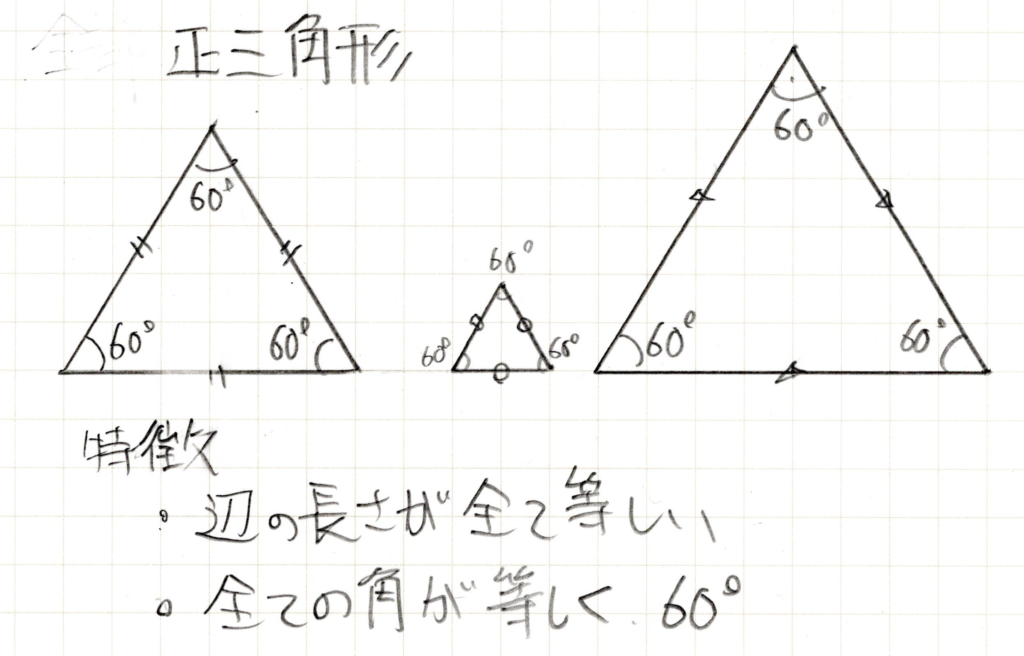
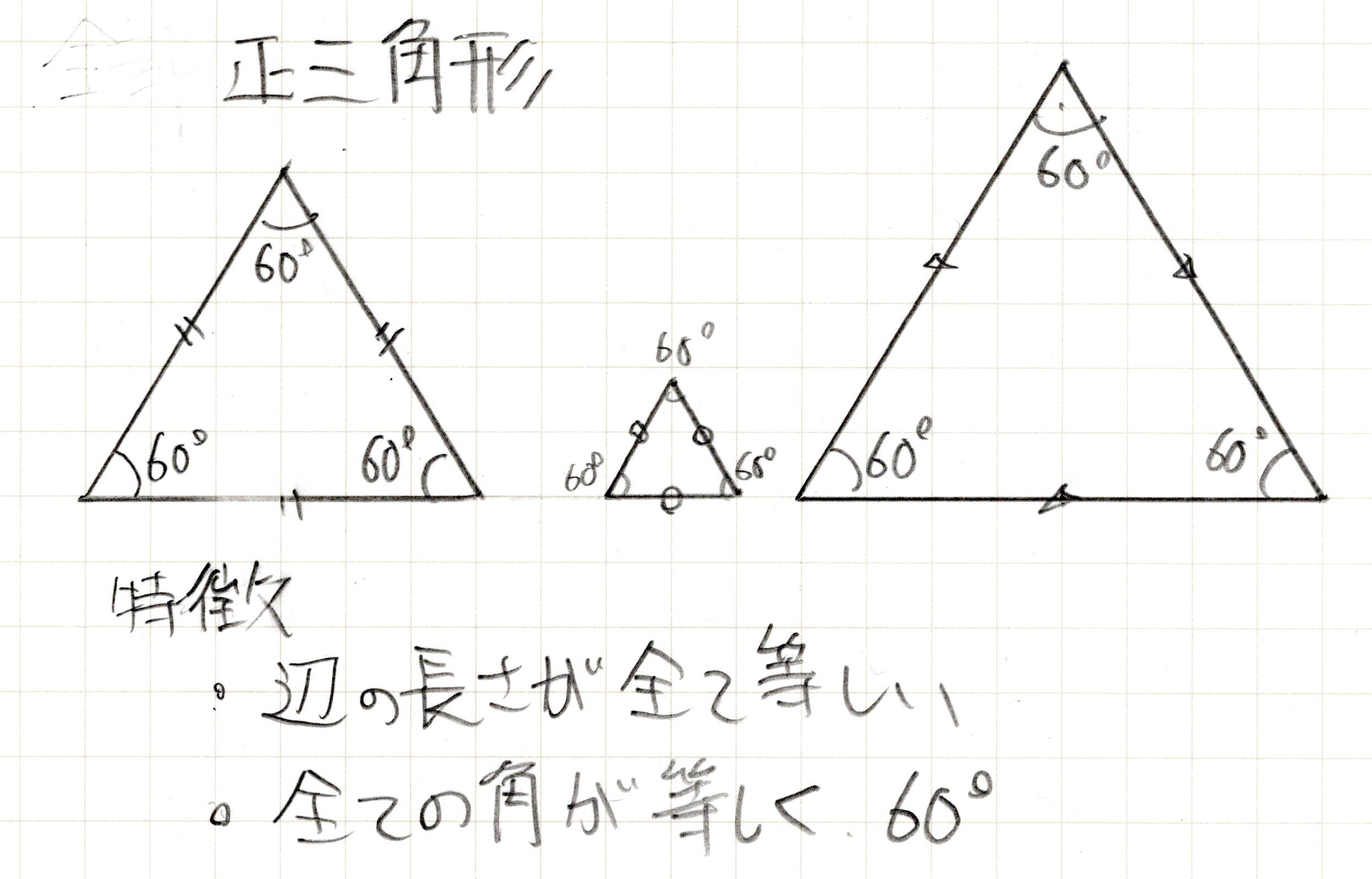
正三角形
全ての辺の長さが同じ三角形です。辺の長さが全て同じであればいいのでどんな大きさでも構いません。
直角三角形
三角形の一つの角度が90°(直角)の三角形です。90°が一つあれば他の角度は何でもOKです。
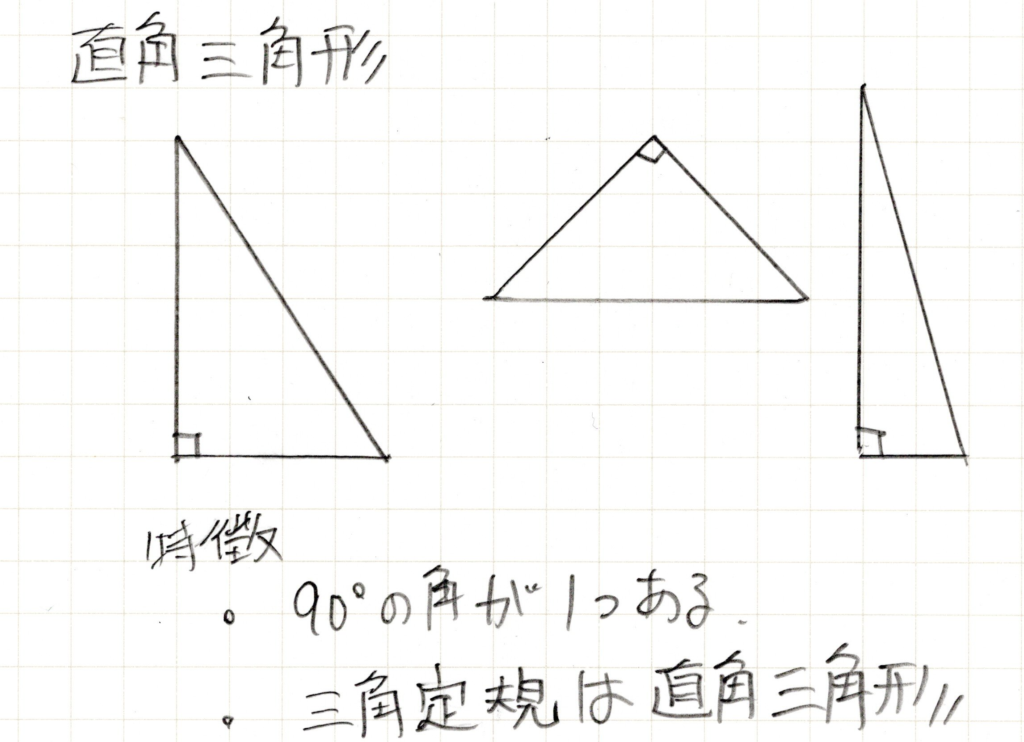
ここで押さえておきたいのは、三角定規はどれも直角三角形ということです。

直角三角形と言われたら、筆箱の中を見てどんな三角形か思い出すようにしましょう。
二等辺三角形
二つの辺の長さが等しい三角形を二等辺三角形といいます。
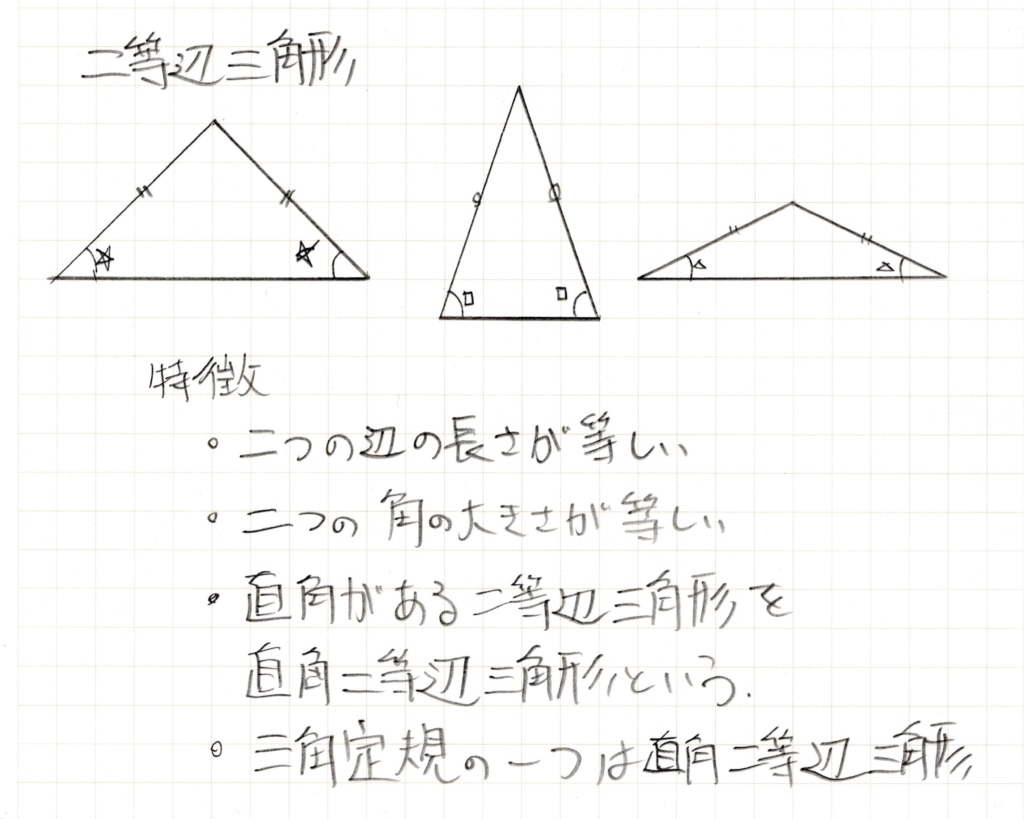
これも三角定規に隠れていますね。低学年の子供にとって、二等辺三角形が一番難易度が高いようです。二辺が等しい、二つの角が等しい三角形ですが、これがなかなか覚えられないようです。
二等辺三角形のスゴ技
スゴ技というほど大したことではないかもしれませんが、二等辺三角形はどれか一つの角度がわかれば、全ての角度がわかってしまうという、算数の問題を解くのに非常に便利な技があります。
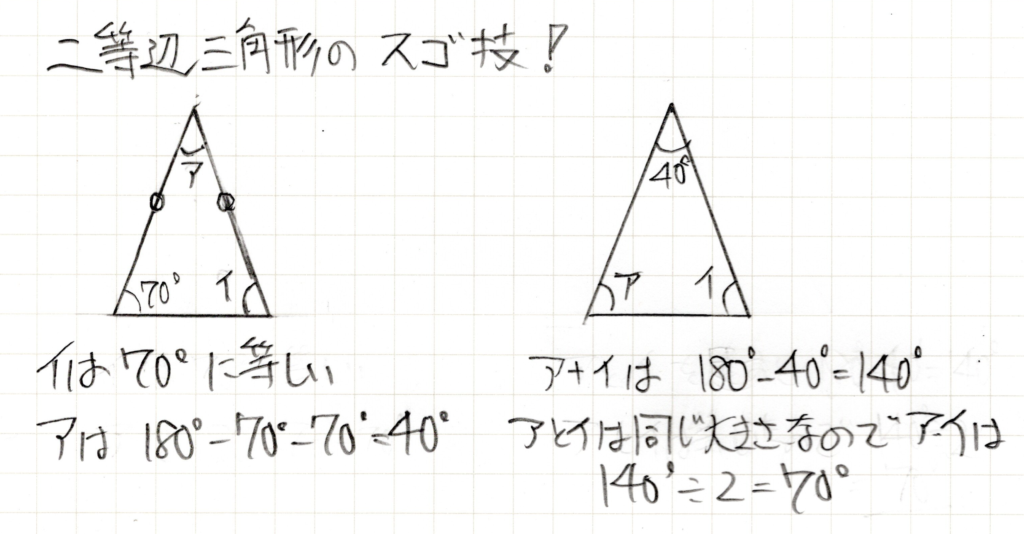
このように、二等辺三角形の一つの角度がわかれば全ての角度がわかってしまうのです!って、すみません、私がおぉって思っているだけで、普通のことかもしれません。。。
角度の問題へのアプローチ
角度の問題を解く時、いつも思うのが、隠れているなじみの図形に気づくことが解くのに大事だなということです。なじみの図形とは、ここでは上で説明した正三角形や二等辺三角形など特徴をよく把握した図形のことを示しています。
慣れてくれば補助線を引いたりして、なじみの図形を探していくのですが、慣れない内は、問題の図形から確実になじみの図形、特徴をよく知った図形を見つけるところから始めていくのがよいかと思います。
問題 なじみの三角形を探す
問題
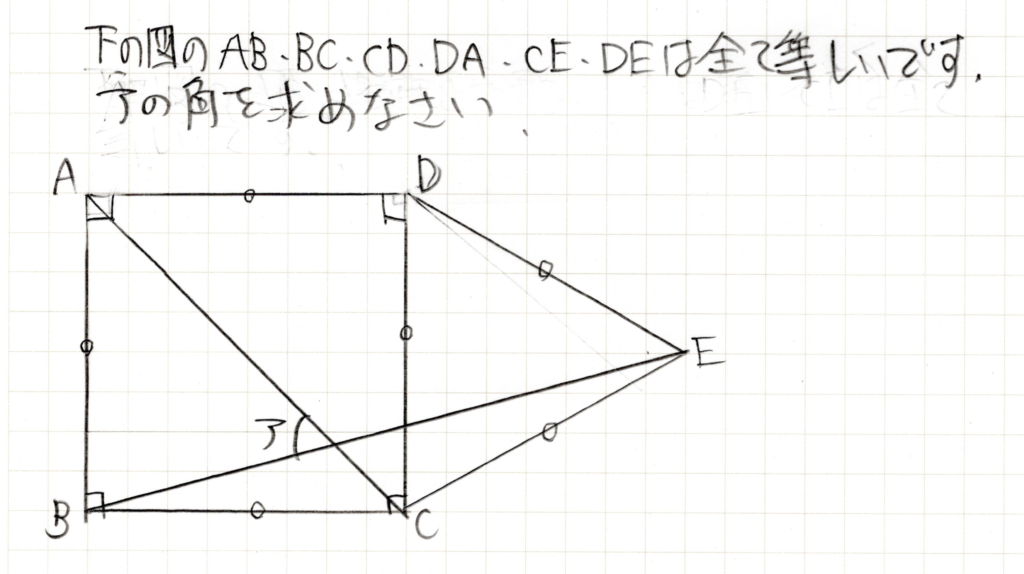
一見、複雑で難しそうな問題ですが、角度を求めることは一旦おいておいて、なじみの三角形を見つけることに注力します。直角二等辺三角形と正方形、二等辺三角形あたりが見つかるでしょうか?
解答
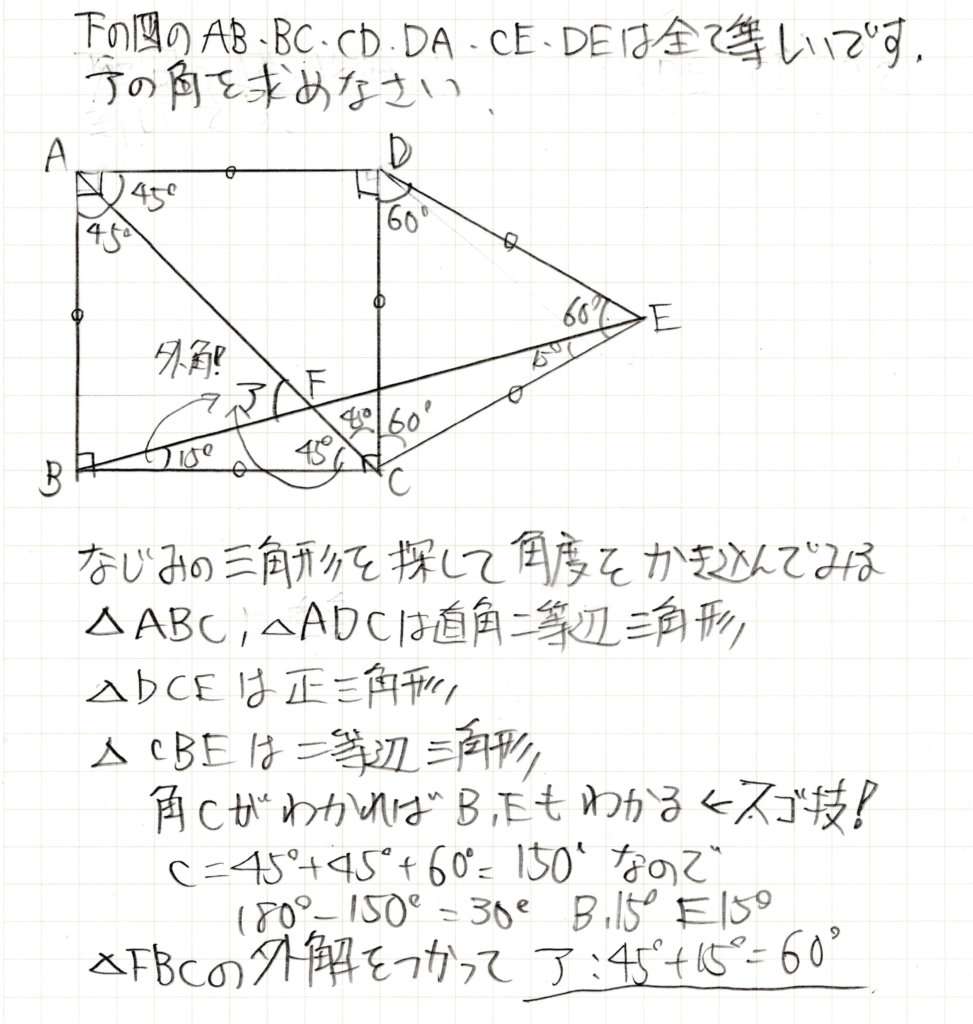
わかりやすいように記号Fも追加しています。とにかく三角形を見つけて、それがなじみのやつかどうかかたっぱしから判断し、なじみのやつであればわかる角度を入れていきます。(答えの外角が外解と間違っていますね。。すみません。)
三角形を見つけるというのは幼児教育などで行う、パズルに近い感覚です。その三角形が知っている三角形かそうでない三角形かの判断が小学校低学年では求められるスキルになるかと思います。
探す過程で△AFBなどについても考えてみればいいのです。それが、二等辺でもなければ直角でもない、なじみのない三角形かどうかを判断して、知らない三角形でなければ、とりあえずほおっておけばいいです。
そういう、探す→見つける→書き込むを繰り返して、情報を明確にしていくことが一番大事です。もちろん、答えにたどり着ければ素晴らしいですが。
前回学習した外角を最後使っています。内角の和でももちろん出せます。色々な答えの出し方を調べてみるのも面白いかもしれません。
まとめ
今回は三角形の種類について学びました。まずはしっかり3種類の三角形とその特徴を覚えるとよいでしょう。
どうしても覚えられないような場合は、三角形が身の回りのどこにあるか?それは何三角形かを探すゲームなどしてもよいかもしれません。正三角形は5点、二等辺三角形は3点、直角三角形は1点のように競って遊ぶような方法もあります。
そして三角形を応用した角度の問題を解いてみましょう。最初は解けなくてもOK。しっかりなじみの三角形をさがして、情報を書き込んでみましょう。大人でも頭が固いと難しい問題もありますので、子供と一緒になって三角形探しをしてみてはいかがでしょうか?
前回の記事はこちらから。
次の記事はこちらから。

コメント