【低学年向け 中学受験 に向けた算数】素数と素数の活用について 【第１１回】

　今回のテーマは素数です。正直、一番説明が難しく、何の役に立つのか上手く説明できる自信がないので、筆が重いです。

　前回は倍数、約数、について学んだのですが、その倍数、約数の問題をより解きやすくするための考え方　というところからアプローチしていこうと思います。

　なるべくわかりやすく説明しますので、わからなくなったら是非ここに立ち返って思い出していただければと思います。

　この記事はうちの子が３年生で学習した算数を振り返り、解説を備忘録的にまとめておこうというシリーズ。教え方は学校の先生、塾の先生、親など教える人それぞれだと思いますので、参考程度にみていただければと思います。

　中学受験 は算数がキモといっても過言ではありません。論理的思考はどの教科を学ぶにおいても重要となる、鍛えておくべき力だと個人的には思っています。

　問題・解答はPCで作図するより手書きが一番早いので、手書きでまとめています。少々見辛い箇所もあるかと思いますが、ご了承ください。

　前回の記事はこちらから。

素数

素数とは？

　素数は１とその数自身しか約数（割り切れる数）がない数のことです。例えば、７は割り切れる数が１と７だけです。１とその数自身（７）しか約数がないので、７は素数になります。

　一方、６は約数が１，２，３，６となり、１と６以外にも約数が存在します。なので、６は素数ではありません。また、数字の１は約数は１だけなので、素数ではないことに注意してください。

素数の調べ方

　ある数が素数であるかどうかの調べ方ですが、手堅く順に割り算をして調べていくのが良いです。例えば４３という数が素数かどうか調べてきます。

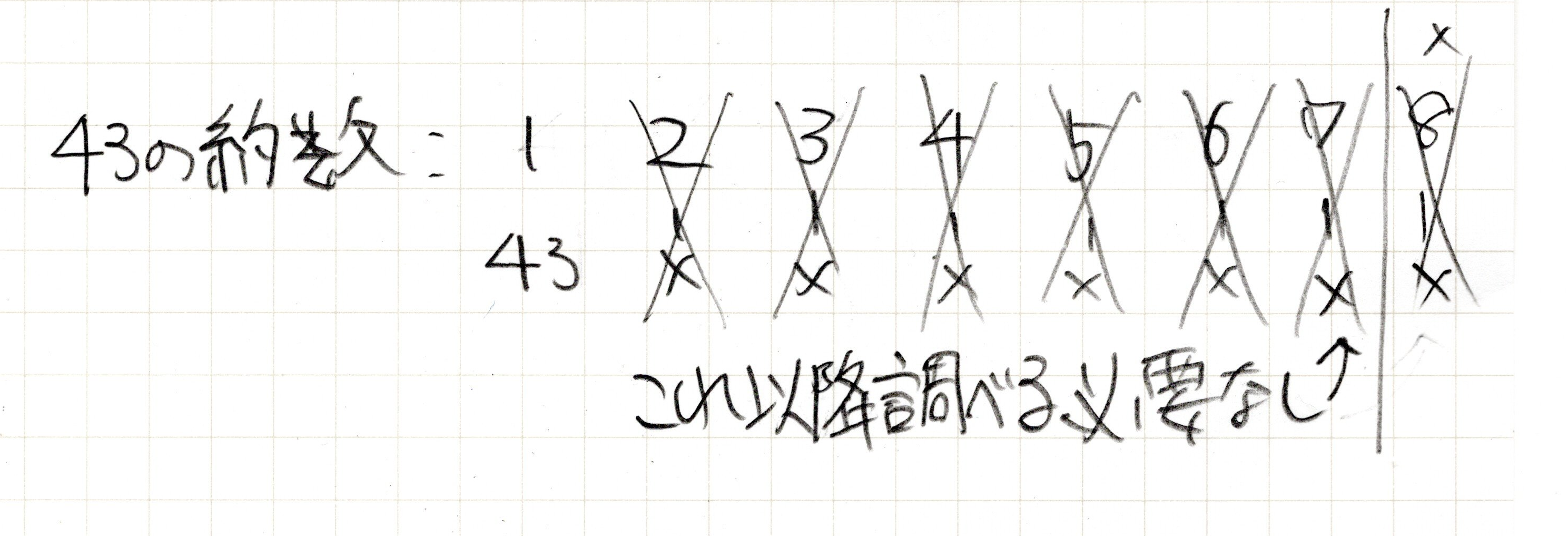
　前回、説明した約数の調べ方と同じように、ペアを考えて調べていきます。

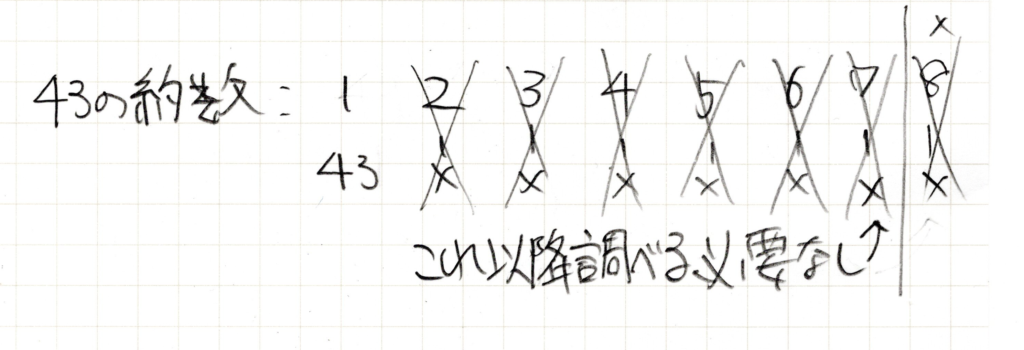
　このように、７までは１と４３以外に割り切れる数がないので、約数ペアは１つしか見つかりません。そして、この場合、７以降は調べる必要はありません。なぜなら、もし、８で割り切れるならこれより前にどこかのペアで出てきているはずだからです。

　８で割り切れた時、商は５，６位になり、その数はすでに調査済みで辺りのペアで出てくるはずです。９以降も同様に、割り切れるとしたらとっくにペアで出てきているはずですので、調べるのは不要です。約数を調べる時はペアで調べ、折り返しを意識して調べるようにすることで、無駄なくもれなく調べることができます。

素数の活用

素因数分解

　では素数は何の役に立つのでしょうか？割れる数が２つしかない、だからどうした？と思うでしょう。素数は約数、倍数、最大公約数、最小公倍数を調べるのに役に立ちます。

　ある数を素数のみのかけ算で表現することを素因数分解といいます。言葉は難しいですが、調べ方は簡単で、約数を見つけていくやり方に似ています。例として１０５を素因数分解してみます。

　　１０５＝３×３５
　　　　　＝３×５×７（３５＝５×７）

　このように、２で割れるかな？３で割れるかな？５で割れるかな？と調べていき、徐々に式を素数のみに変換してきます。１０５を素因数分解すると３×５×７になることがわかりました。

　ただ、まだこの段階では「素因数分解して何が嬉しいのか？」、「何がいいことがあるのか？」わからないかもしれません。

最大公約数を調べるのに便利

　さて、１０５＝３×５×７に素因数分解しましたが、１０５にはどういった約数があるかを考えます。３，５，７は約数になるのは素因数分解の結果を見れば明白です。では１５は約数でしょうか？どうでしょう？

　１０５の素因数分解の中に３×５（＝１５）が含まれているので、１０５は１５で割ることができるます。素因数分解により、約数かどうかの判断が一目でわかるようになります。

　同様に２１はどうでしょう？３×７（＝２１）が含まれているので、２１も約数となります。このように素因数分解した結果から約数を調べることができました。

　次に素数活用の真骨頂、ある二つの数の最大公約数を素因数分解を使って求めてみます。

例として、１２６と２１０の最大公約数を考えてみます。まずはこれらの数を素因数分解してみます。結果は以下のようになります。

１２６＝２×３×３×７
２１０＝２×３×５×７

改めて、公約数とはこれら二つの数を両方とも割り切れるような数でした。２１０は５や１０で割れることは、先ほどの説明からすぐにわかるかと思いますが、１２６は５や１０で割れるでしょうか？

１２６は素因数分解に５が含まれていないので、５や１０では割れない、すなわち、５や１０は約数ではないことが素因数分解の結果から確認できます。

一方、１２６は３×３が含まれているので、９でわることができますが、２１０はどうでしょう？

２１０は３が一つしか含まれていないので、９で割ることができません。９で割るためには素因数分解の結果にもう一つ３が必要です。すなわち９は２１０の約数ではないことが素因数分解の結果からわかります。

最後に６や２１はどうでしょう？１２６、２１０共に素因数分解の結果に２×３、３×７が含まれているので、６、２１は公約数になることがわかります。

このように、１２６、２１０の公約数になるためには、１２６、２１０を素因数分解した結果において、お互い共通して持っている素数をかけてできる数である必要があります。

「２が一個」、「３が一個」、「７が一個」のいずれかを掛けてできる数（例えば６や１４）は公約数になり、「５」や「３を二個」使ってできる数（例えば１０や９）は公約数にならないのです。

これを踏まえて最大公約数を求めてみます。素因数分解の結果で共通している数を全部掛け合わせたものが公約数かつ最大になるので、

２×３×７＝４２　が１２６と２１０の最大公約数となることがわかります。

　余談ですが、「何で素数のかけ算で表す必要があるの？」というのがここまでの解説で少し分かっていただけたかと思います。

　例えば１２６＝２×９×７と９を素因数分解し忘れた場合、３が含まれていることに気づくことができず、共通の数字は２と７で最大公約数が２×７＝１４であると間違って判断してしまうことになります。

　また、３を見逃すことで、１２６は６（２×３）で割れますか？という問題を間違って割れないと判断してしまうかもしれません。

　もうこれ以上ばらばら（割り算）できない、９も３×３まできっちり素数にまで分解しておくことで、その数がどういうかけ算で構成されているのかを丸裸にすることができます。これ以上分解できないというのがミソです。

最小公倍数を見つけるのに便利

　素因数分解で数の構造を調べるという感覚が少しわかりはじめたでしょうか？続いて最小公約数を調べてみます。数は先ほど同じ１２６と２１０にします。

　あらためて、１２６と２１０の素因数分解の結果は以下でした。

１２６＝２×３×３×７
２１０＝２×３×５×７

　さて、１２６の倍数は１２６を何倍かしたもので２１０の倍数は２１０を何倍かしたものです。公倍数はそれぞれ何倍かして同じ数になった１２６と２１０が共通で持つ倍数のことでした。

　言い換えると、１２６と２１０の公倍数は１２６でも割れて、２１０でも割れる数ということになります。

　ではその公倍数の素因数分解を考えた時、どんな数が入っているでしょうか？公倍数は１２６で割れるので２×３×３×７は絶対に含まれているでしょう。また、２１０で割り切れるので、２×３×５×７は絶対に含まれているでしょう。

　すると、とある公倍数はこんな感じになっているのかなぁ？と想像できます。

　１２６と２１０のとある公倍数　＝　２×３×３×７　×　２×３×５×７

　ただ、この公倍数は最小ではないですね。３は合計３個含まれていますが、２個で十分なはずです。１２６で割り切るためには３が２個あればよく、２１０で割り切るためには３が１個あればよいので、２個あれば事足ります。同様に、２や７も１個あれば共通で使えます。すなわち

１２６と２１０の最小公倍数　＝　２×３×３×７　×　２×３×５×７

　のように、重複してる数を消すと２×３×３×７×５＝６３０が最小公倍数になることがわかります。この式には１２６＝２×３×３×７も２１０＝２×３×５×７も含まれています。

手順のまとめ

　ここまでだらだらと解説を書きましたが、最大公約数、最小公倍数を素因数分解を使って求める手順をまとめておきます。

　手順をまとめると短いですが、なぜそうなるか解説を読んで理解しておくことが大事です。

まとめ

　素数は素人の私では非常に説明が難しいです。また理解にも前提の知識が結構必要で、例えば６＝２×３になるから６は２で割れるね。という感覚が身に付いている必要があります。

　低学年の内は素因数分解させるようなパズルで感覚を養うといいかもしれません。中学への算数という書籍のパズルコーナーによくそういったパズルが掲載されていますので、挑戦されてみてはいかがでしょうか？

　前回の記事はこちらから。