今回のテーマは約数と倍数です。これまで、いろんな図形、角度について学んできましたが、いったん図形から離れます。低学年にとっては約数と倍数はどっちがどっちか、最大か最小か?など色々ごっちゃになりやすく混乱しやすい内容です。
なるべくわかりやすく説明しますので、わからなくなったら是非ここに立ち返って思い出していただければと思います。
この記事はうちの子が3年生で学習した算数を振り返り、解説を備忘録的にまとめておこうというシリーズ。教え方は学校の先生、塾の先生、親など教える人それぞれだと思いますので、参考程度にみていただければと思います。
中学受験は算数がキモといっても過言ではありません。論理的思考はどの教科を学ぶにおいても重要となる、鍛えておくべき力だと個人的には思っています。
問題・解答はPCで作図するより手書きが一番早いので、手書きでまとめています。少々見辛い箇所もあるかと思いますが、ご了承ください。
前回の記事はこちらから。
次の記事はこちら。
倍数
まずは倍数の説明からです。ある数Aがあるとします。その数Aを1倍、2倍、3倍、4倍とした数、全てがAの倍数です。
例えば、3の倍数は3,6,9,12,15・・・と続いていきます。3を二倍、三倍と倍々にしていっています。
5の倍数だと5,10,15,20,25・・・です。5を二倍、三倍と倍々にしていっています。
覚え方としては、倍数は倍という字が入っているので、その名の通り、倍々にした数という風に覚えるといいでしょう。
約数
ある数Aがある時、その数Aを割り切れる数が約数です。
例えば、8の約数は1,2,4,8です。8は1,2では割り切れても3では割り切れません。なので、3は約数にはなりません。同様に、6,7でも割り切ることはできませんので、これらも約数にはなりません。
倍数はかけ算、約数は割り算と覚えておけば、ごっちゃにならないと思います。
また、倍数はどんどん無限にでてきますが、約数は無限に出てきません。
最小公倍数
ある二つ以上の数の倍数の内、共通して同じ数になるものを公倍数といいます。???だと思うので、例を考えた方がわかりやすいです。
たとえば、3と4の公倍数を考えます。
3の倍数:3,6,9,12,15,18,21,24・・・・ と続きます。
4の倍数:4,8,12,16,20,24,28・・・・ と続きます。
となるので、公倍数は両方で共通に持っている倍数 12、24・・・となります。・・・と書いたのは無限に続くからです。36,48,60,72,84・・・・と。これら全て3と4の公倍数です。
で、最小公倍数は公倍数の中で最も小さい公倍数なので、3と4の公倍数で最も小さい12が3と4の最小公倍数となります。
ここで、最大公倍数だっけ?最小公倍数だっけ?どっちだっけ?と、わからなくなることがあるかもしれません。覚え方としては倍数は無限に大きくなっていくので、
倍数のどんどん大きくなるので、最大なんかいくつになるかわからない!
→だから最大公倍数を求めるのは無理
→だから求めるられるのは最小公倍数!
という流れで、最大か最小か思い出してみてはどうでしょう。
最大公約数
ある二つ以上の数の約数の内、同じ数の約数を公約数といいます。???だと思うので、例を考えた方がわかりやすいです。
たとえば、12と18の公約数を考えます。
12の約数:1,2,3,4,6,12
18の約数:1,2,3,6,9,18
となるので、公約数は両方で共通に持っている約数、1,2,3,6が公約数となります。
そして、その公約数のうち、最大のものを最大公約数といいます。この例だと最大公約数は6となります。
ここで、最大公約数だっけ?最小公約数だっけ?どっちだっけ?とわからなくなることがあるかもしれません。覚え方としては、
どんな数の約数でも最小は必ず1
→だから最小公約数があるとすると答えはかならず1になるので、求めるの簡単すぎ!
→だから考えないといけないのは最大公約数!
多少強引な覚え方ですが、最大、最小、倍数、約数の組み合わせがごちゃごちゃにならないようにしましょう。
問題1 公約数をみつける
問題

解
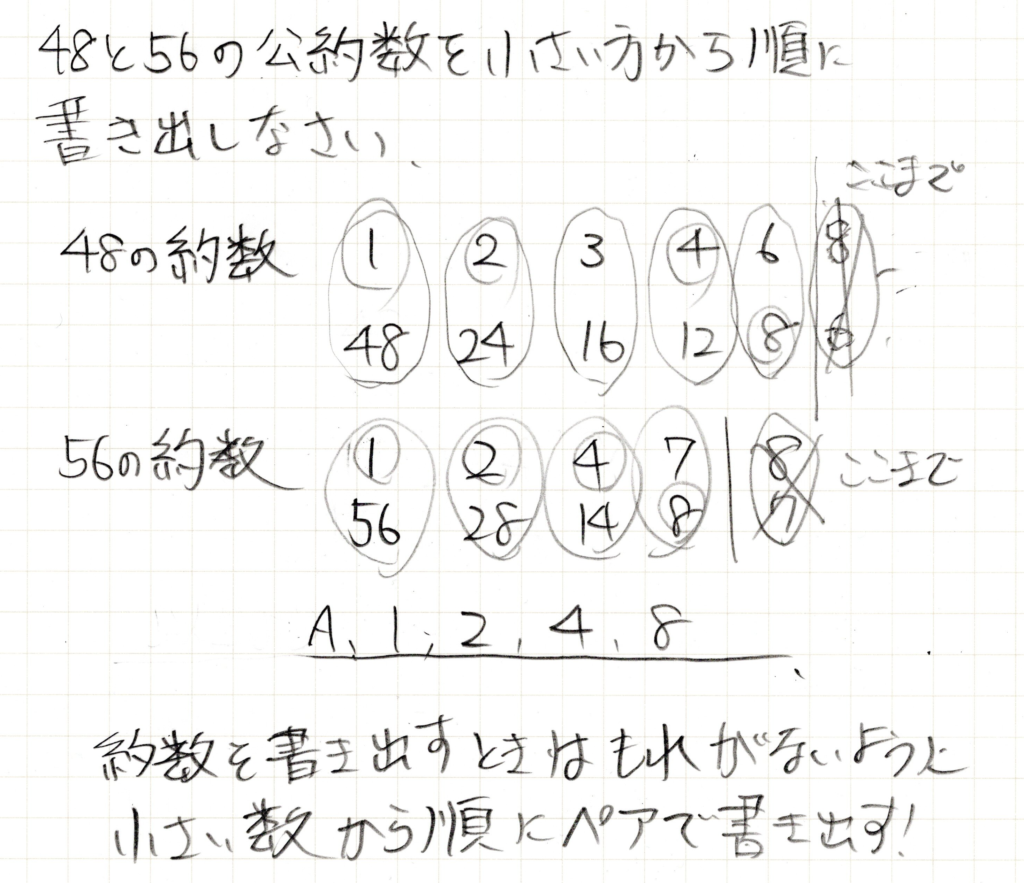
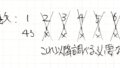
約数を書き出していくのですが、適当に書き出すと絶対漏れが生じてしまいます。ここでは約数を漏らさず書き出す方法をご紹介します。
上の48の約数を例に説明します。まず1から割り切れる数を探していくのですが、割り切れる数を見つけたらその時の答えもペアとして書き出しておきます。1の時は48、2の時は24といった具合にペアで書き出します。
なぜなら、割った答えもその数の約数になるからです。そして、6と8をペアにしたら次は8と6になりますが、それは前の6と8で同じなので、ここで探すのをやめます。
こうすることで、約数を書き出す漏れを防ぐことができます。
問題2 最小公倍数をみつける
問題

解

まとめ
まずはしっかりともれなく倍数、約数を書き出せるようになりましょう。漏れなく書き出せるというのは最低限必要な技術です。特に約数はペアで書き出すことがなぜもれなく書き出せるのか?を論理的に理解できれば完璧です。
もちろん、低学年の内は数字を小さい方から割っていき、ペアで書き出していく方法に慣れることから始めればいいと思います。
前回の記事はこちらから。
次の記事はこちら。

コメント