今回のテーマは角度です。2本の線(辺)がくっついて作られる形を各、その大きさを表すのが角度です。色々な角度を求めてみます。
この記事はうちの子が3年生で学習した算数を振り返り、解説を備忘録的にまとめておこうというシリーズ。教え方は学校の先生、塾の先生、親など教える人それぞれだと思いますので、参考程度にみていただければと思います。
中学受験 は算数がキモといっても過言ではありません。論理的思考はどの教科を学ぶにおいても重要となる、鍛えておくべき力だと個人的には思っています。
問題・解答はPCで作図するより手書きが一番早いので、手書きでまとめています。少々見辛い箇所もあるかと思いますが、ご了承ください。
前回の記事はこちら。
次の記事はこちら。
最初に知っておきたい角度
角度とは何か?についてはここでは詳しく話しません。学校でも習うと思いますので。簡単に下にまとめておきます。
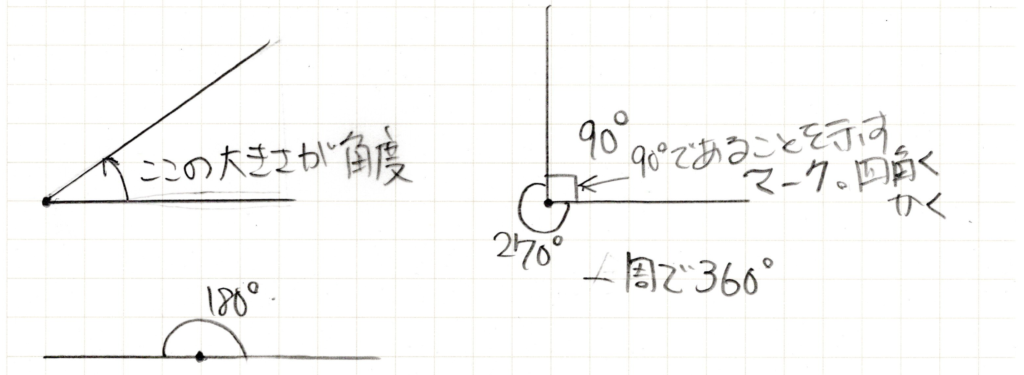
90°は別名直角とも言います。真横に線を引いた時、天に昇っていくような真上の線は90°ですね。(適当すぎる説明・・・)
知っておきたい大切な角度があります。学年が進むにつれて覚えておきたい角度は増えていくのですが(例えば108°、15°みたいな問題へのアプローチには必須の角度)、ここでは最初に最低限覚えておきたい角度とその大きさの感覚についてまとめます。低学年向けなので。
みんな持ってる三角定規。小学生なら必ず買わされるものです。なぜこの形をしているかというと、便利だからです。なぜ便利かはおいおいわかってきます。

角度を書き込むとこんな感じです。最初は「90°って真上になる角度なんだ」とか「30°って尖ってるな」とかそういう感覚だけでも大丈夫です。90°が地面から真上に上がっている大きさでそれを基準にして以下のような感覚が持てればOKです。
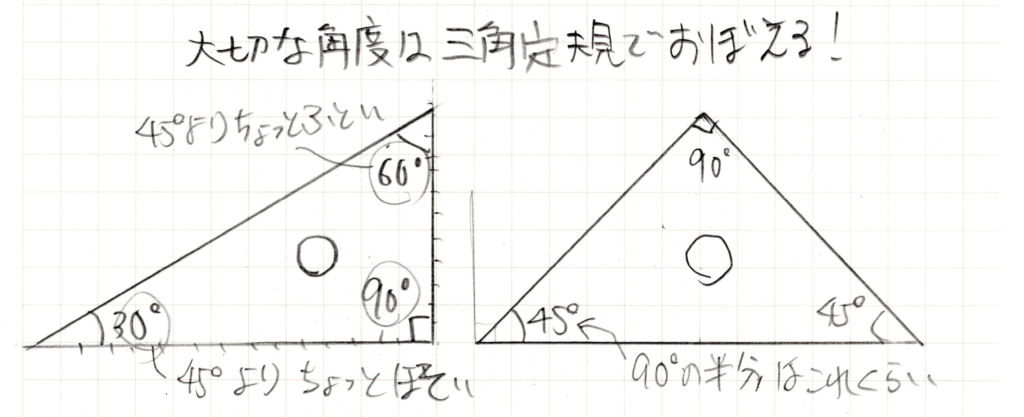
この30、60、45、90に加えて上で説明した360、180という角度も覚えておいてください。
水平と垂直
水平
まっすぐな線(辺)を自由に二本引いてみます。
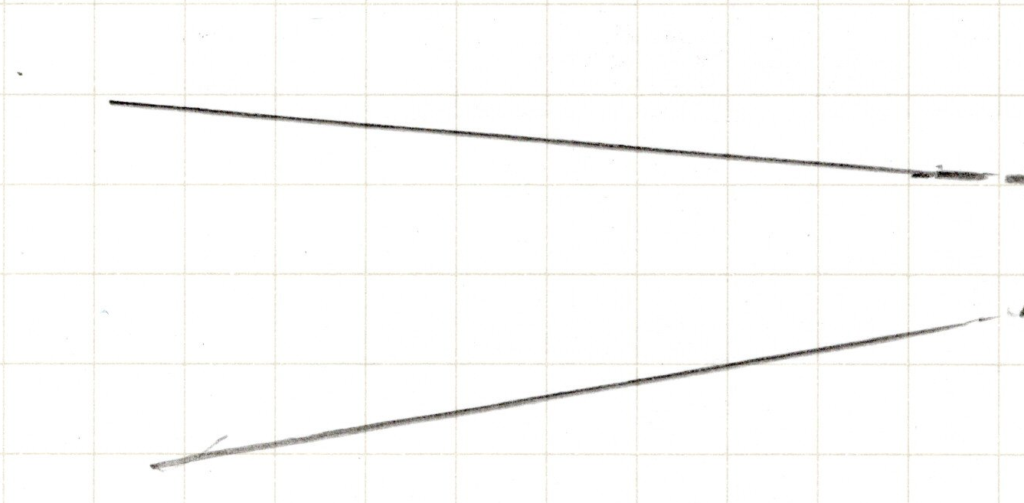
この線は延長するどうなるでしょうか?はい、交わります。
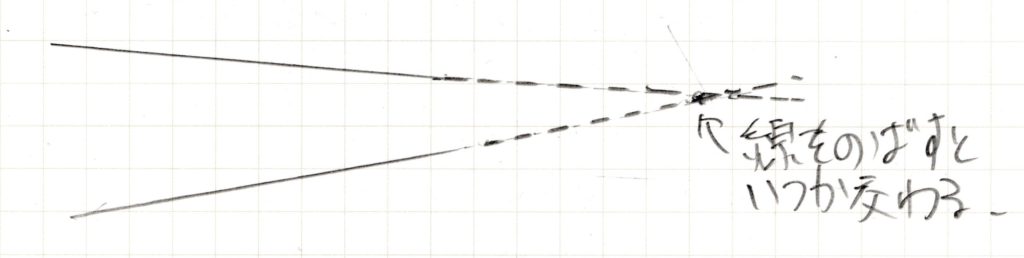
ではこちらはどうでしょう?

ずーっと伸ばしてみると。

交わりません。こういう交わらない二本の線は互いに平行といいます。平行線を引くというのは二本の交わらない線を引くこと、ある線に対して平行な線を引くというのはある線に対して平行となるような線を引くということ。
低学年はこの平行という言葉や線の関係をとにかく覚えません。(うちの子だけかもしれませんが)平行という言葉も聞きなれない言葉ですし、後で説明する垂直という言葉と混在もします。角度の問題でよく出てくるという共通点でごっちゃになってしまいがちです。
どこまで行っても交わらない二本の線。行くという漢字が入っているので平行っていう覚え方はどうでしょうか?うちではこの覚え方ではだめでした。
垂直
うちでは平行と混同される垂直です。垂直は交わると直角になる二本の線の関係のことを言います。この線とこの線は垂直に交わるというような使い方をします。
直立不動で起立をしているので、90°は垂直というのはどうでしょう?これもうちではだめでしたが。
平行な2本の線に交わる線(最強ルール)
この決まりは低学年の角度の問題を解くに当たって絶対に覚えておかなければならない決まりになります。序盤の難し目の問題はこれをきっちり使いこなせるかどうかにかかっているといっても過言ではないです。
その決まりがこちら。
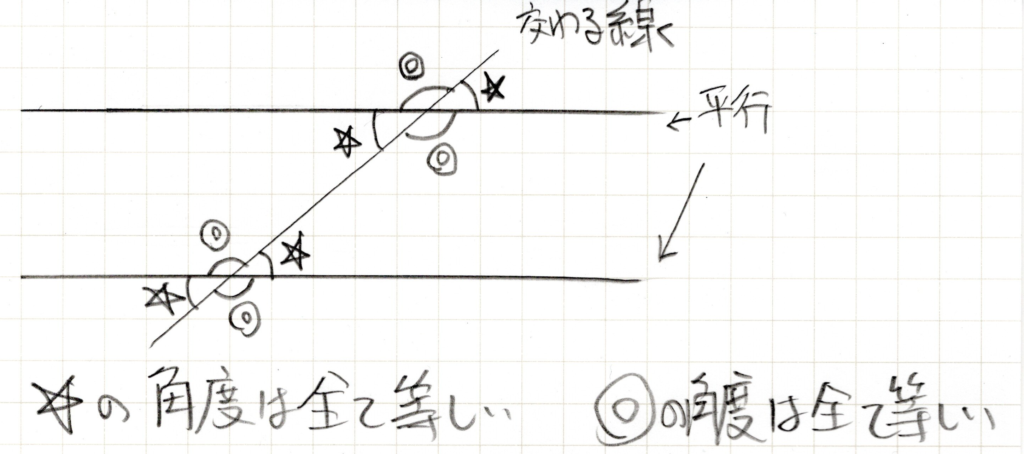
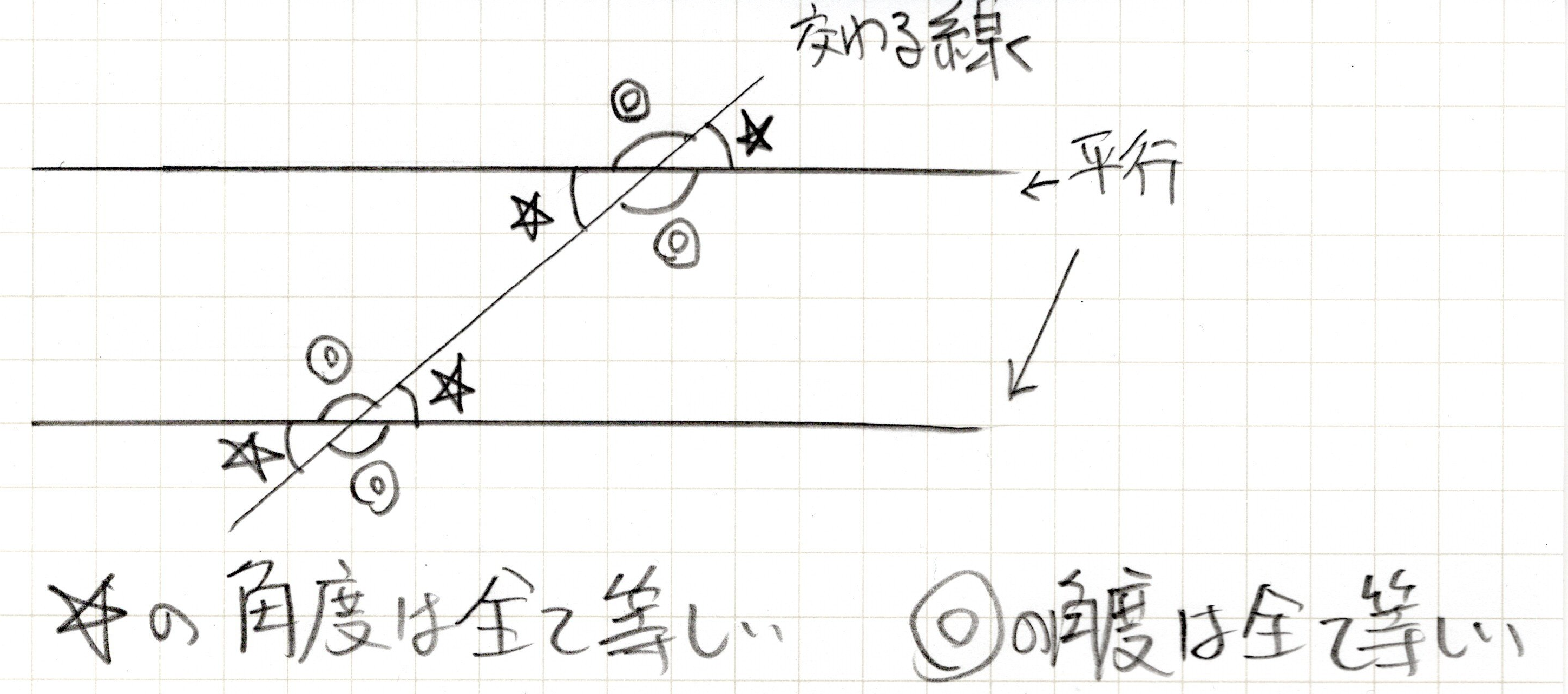
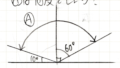
平行の線に交わるように一本線を引き、その時の角度の関係を表しています。☆は全部等しく、◎も全部等しいです。また◎+☆は絶対180°になるというのもポイントです。
あたりまえじゃん。と思う人もいるかもしれませんが、これがそのまま問題に出てくることはありません。隠れているのです。隠れミッキーのように隠れているのを見つける必要があります。例えば。
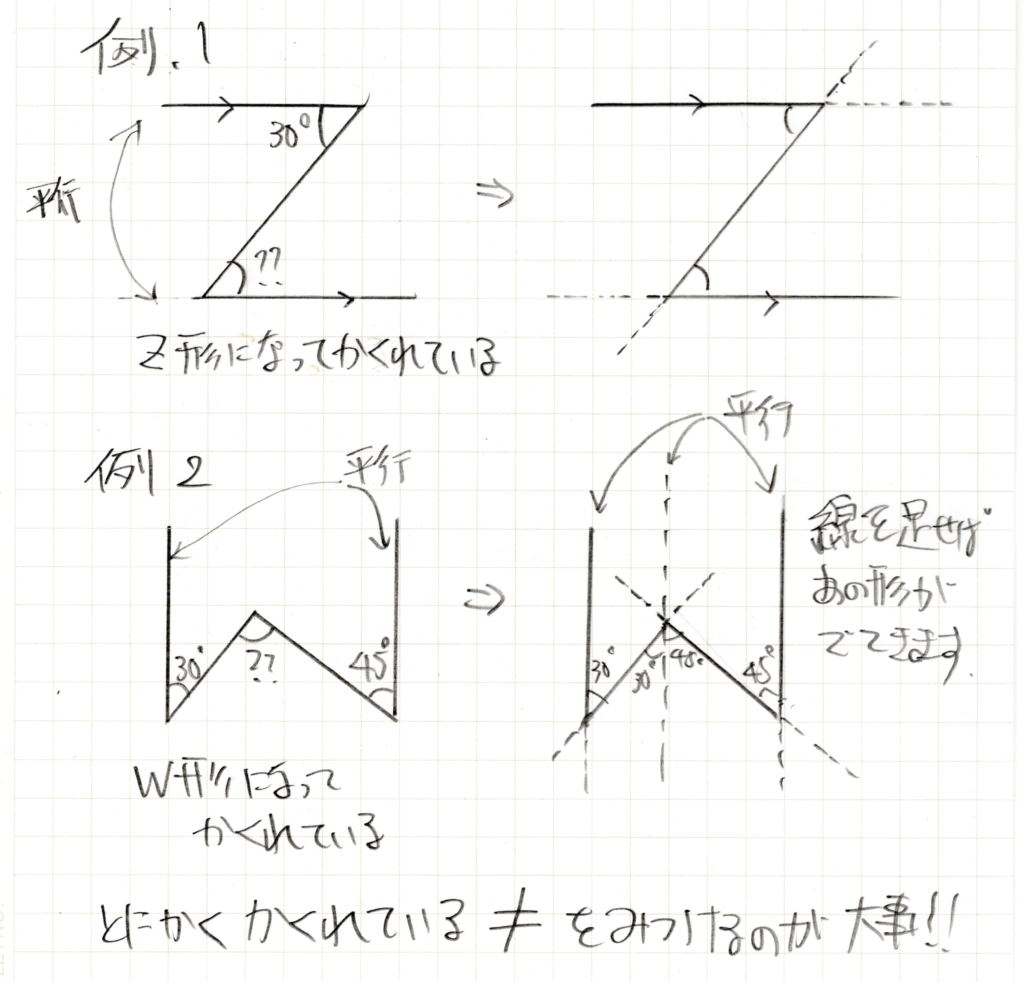
≠が隠れまくっているのです。角度の問題で平行に気づいたら≠を探し回る。低学年の内は最強の立ち回りの一つになる気がします。
まとめ
今回は角度のお話しで例題なしの説明のみでした。≠を見つけることはかなり大事で時に向きを変え、時に線を足し、時に線を伸ばしでとにかく≠を見つけ出すことが大事です。
また、本ブログでは実際に子育て、教育をしないと絶対に体験できない観点も含めています。例えば水平、垂直が混同するなんてのは問題集を執筆しているだけでは絶対にわからないと思うんですよね。そういうリアルな感想も記事に書いていきたいと思っていますので、共感いただけると嬉しいです。
次回以降は角度の問題を解説していきます。低学年で角度マスターになりたい方は是非見ていただければと思います。
前回の記事はこちら。
次の記事はこちら。


コメント