今回のテーマは数の問題の内、差を活用した問題です。これまで数の和、差の基本的なところを学びましたが、差の考え方を活用して問題を解いていきます。
この記事はうちの子が3年生で学習した算数を振り返り、解説を備忘録的にまとめておこうというシリーズ。教え方は学校の先生、塾の先生、親など教える人それぞれだと思いますので、参考程度にみていただければと思います。
中学受験 は算数がキモといっても過言ではありません。論理的思考はどの教科を学ぶにおいても重要となる、鍛えておくべき力だと個人的には思っています。
問題・解答はPCで作図するより手書きが一番早いので、手書きでまとめています。少々見辛い箇所もあるかと思いますが、ご了承ください。
前回の記事はこちら。
次の記事はこちら。
和、差を学んで
第一回目では和、差、線分図といった内容についてまとめましたが、今回は「差」に着目した応用になります。問題のあるひとまとまりの差を意識することで解いていくアプローチです。
低学年の算数なのでスマートに解くのではなく、絵、表、線分図など手を使って泥臭く解いていく方法をメインで進めます。あくまで低学年はスマートに解く必要はなく、問題の本質や仕組みに触れ、コツを学ぶことに注力しています。
和、差は単純に足し算引き算ではなく、全体にどういう差があるのか、足すと全体はどう変わるのかというように、少し広い視点で和差を考えることも大事になります。
問題1 絵を書いてみて差を見つけよう その1
問題

350円グループと360円グループの差は何かに着目する。絵をかいてみるとわかりやすい。
解答

まず、AとBを買ったイメージをつかむために実際にA,Bの個数だけまとめた絵を書いています。
複数の種類のものの数がわからず合計がわかるような問題(ツルカメ算のような)は合計をあらわす情報が複数あるはずなので、そのグループの差に着目しましょう。
この問題はグループの差はAが一個減ってBが二個増えています。そして値段は10円上がっています。このことからA一個よりB二個の方が代金が10円高くなるということに気づけます。冒頭で述べた差は単純な引き算ではないというのはこういうことです。まとまりにどういった違い(差)があるのか、その差が何を生み出しているのかをしっかりとらえられるようにしましょう。
A一個よりB二個の方が10円高くなるので、AをBに置き換えているのが後半の表です。Aが減ってBが二個増える度に代金が10円上がっていっています。計算しやすいように余計なものを置き換え消していくというのも非常に重要な考え方なので、身に付ける必要がある技の一つです。
ここまで書ければあとはBの代金を求めるだけです。
問題2 絵を書いてみて差を見つけよう その2
問題

まずはお絵描きしてみるとよいかもしれません。文字でバーっと書かれているとイメージがつかみにくいです。
解答

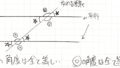
絵をかいてみると「10円+50円」と「50円+100円」を比較することで、合計枚数が2枚変わっている差に気づくかと思います。
50円玉の数は変わらないので、枚数の差はそのままが10円と100円の枚数の差になりますね。
10円と100円の合計がわかっているので、ここで線分図を書きます。線分図はどちらが多いかわかっていない状態だと書きづらい、使いづらいなぁというのがわかると思います。
逆に合計やそれぞれの差がわかっている状態だと線分図は非常に有効であるのも体感できると思います。
また他の解き方として、10円と50円が5枚づつだったらと固定して、他の枚数を調べていくというのも3年生のうちはアリだと個人的に思います。答えが合わない時にどの枚数をどうすれば答えに近づくか?そういった数に対する感覚を養っていくことも重要だと考えるからです。
まとめ
広い視点で違い(差)をみることで細かい情報を明らかにしていくような問題でした。何をどうしたら何が変わったのか?をしっかり考えることで、パズルのように情報を明らかにしていくことができます。
こういった考え方はエンジニアリングでも重要な論理的思考で低学年の内にしっかり学んでおきたい基礎にもなります。
前回の記事はこちら。
次の記事はこちら。


コメント