【低学年向け 中学受験 に向けた算数】多角形【第８回】

　今回のテーマは多角形です。第６、７回では三角形について学びました。三角形とは３つの辺と３つの角を持つ図形だったことを思い出しましょう。ここでは辺や角を４つ、５つと増やした時どんな図形になるのかについて学びます。

　この記事はうちの子が３年生で学習した算数を振り返り、解説を備忘録的にまとめておこうというシリーズ。教え方は学校の先生、塾の先生、親など教える人それぞれだと思いますので、参考程度にみていただければと思います。

　中学受験 は算数がキモといっても過言ではありません。論理的思考はどの教科を学ぶにおいても重要となる、鍛えておくべき力だと個人的には思っています。

　問題・解答はPCで作図するより手書きが一番早いので、手書きでまとめています。少々見辛い箇所もあるかと思いますが、ご了承ください。

　前回の記事はこちらから。

　次の記事はこちら。

多角形とは

　直線で囲うように適当に絵を書いてみます。

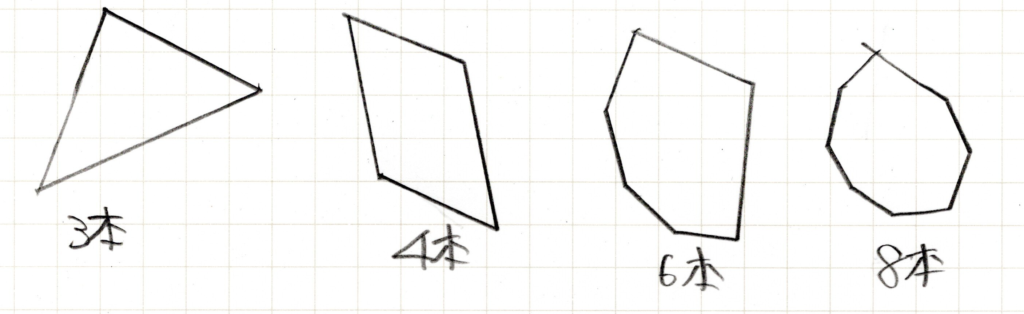
　何本と書かれているのは直線（辺）の数です。当然ですが、２本では囲った図形は描けないので、３本からになります。これらの図形は多角形と呼ばれ、使った直線の本数に応じて名前が異なります。

　直線が３本であれば三角形、４本であれば四角形、６本なら六角形、８本なら八角形です。何角形までも存在します。また、角も辺と同じ数になるということも覚えておきましょう。

多角形の内角

多角形の内角とは

　多角形の内側には角があり、それをそれぞれ内角といいます。三角形には３つの内角、四角形には４つの内角というように〇角形には〇この内角があります。

多角形の内角の和

では、多角形の内角の角度の合計はいくつになるでしょうか？調べる前に復習になりますが、三角形の内角の和は180°でした。それは以前の記事でまとめています。

　三角形の内角の和が180°になることを利用して多角形の使って調べていきます。まず四角形を調べてみましょう。

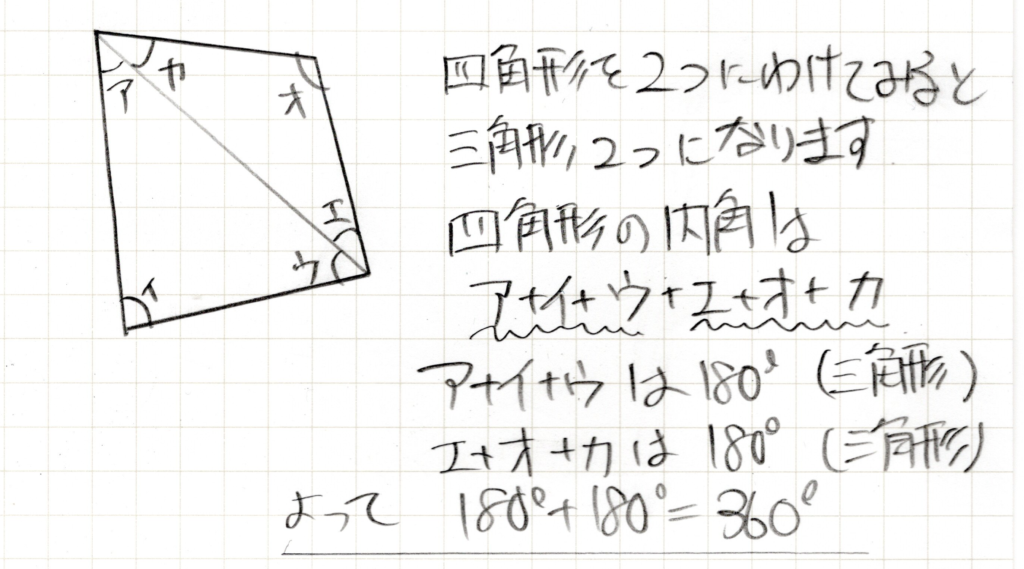
　四角形を直線で二つにわければ三角形が二つになります。三角形の内角の和は180°でそれが二つあるので、角度の合計は360°となります。すなわち、四角形の内角の和は360°ということがわかります。

　どんな形の四角形でも内角の和は360°です。潰れた四角形も真四角もどんな形でもです。

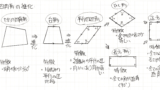
　同様に他の多角形も見てみましょう。

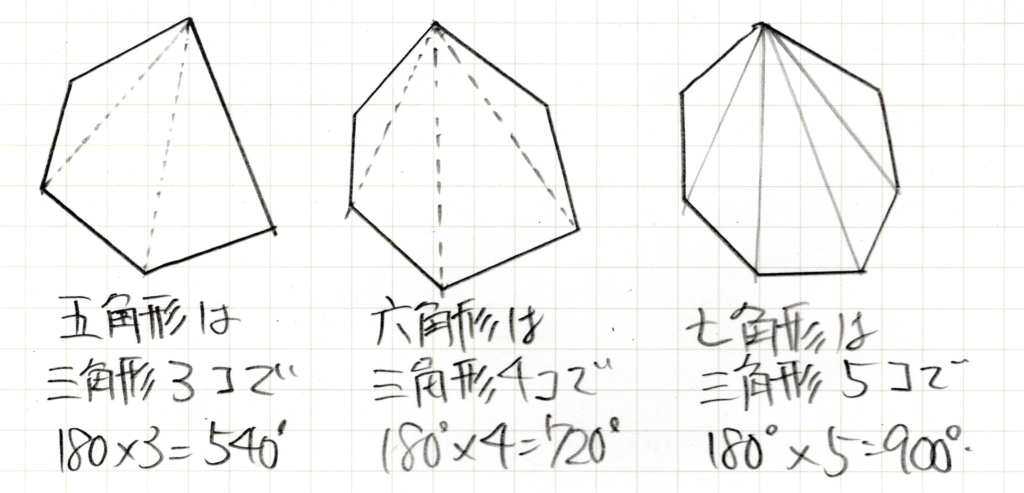
　このように、多角形の一つの頂点から三角形に分け、三角形の内角の和を使って計算すれば多角形の内角の和がわかります。

多角形の外角

多角形の外角とは

　多角形にも三角形と同じように外角があります。ある角を作っている辺を延長してそこにできる外側の角のことです。

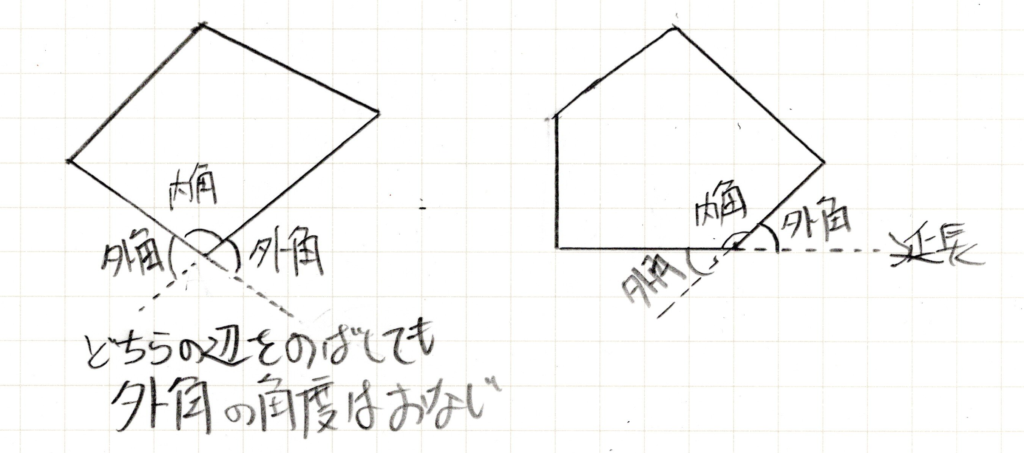
どちらに線を伸ばしても外角は同じになります。

多角形の外角の和とは

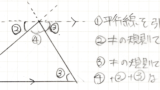
　多角形の外角の合計はいくつになるでしょうか？色々な求め方がありますが、一番直感でイメージしやすいものをご紹介します。

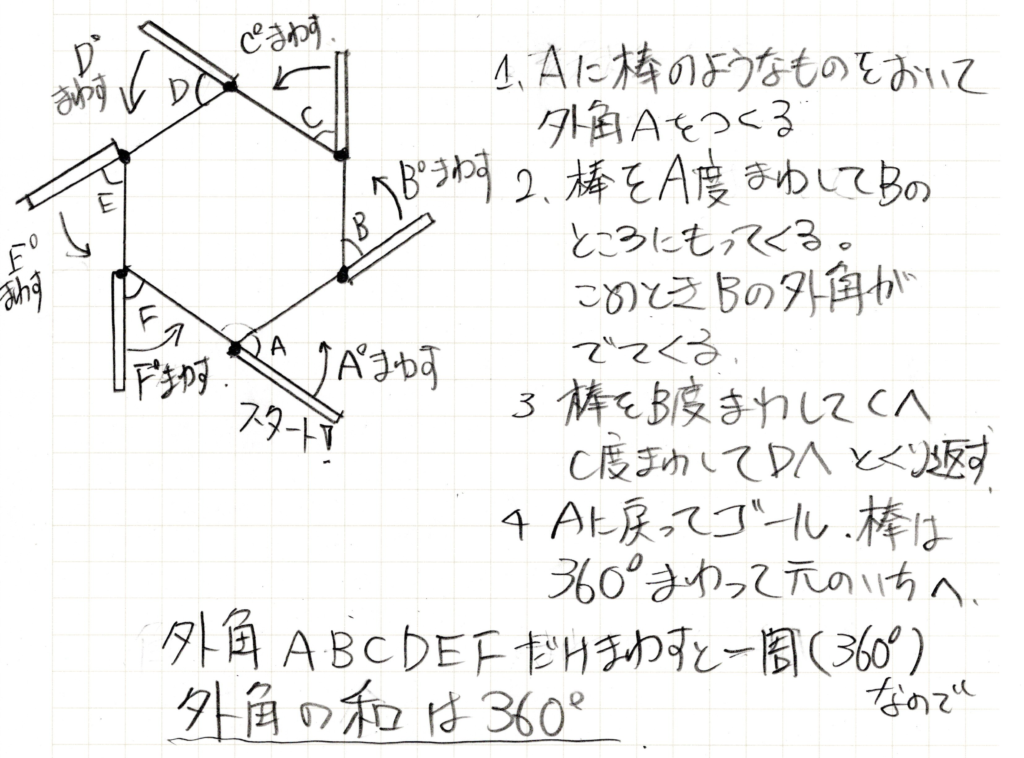
　このように、棒のようなもので辺を伸ばして外角分だけ回す→次の角へ→また外角回す・・・　を繰り返すと、必ず最初の棒の位置に戻ってきます。棒がくるりとちょうど一周回って戻ってくるので、外角の角度を全部回すと一周（360°）となることがわかります。

　すなわち外角の和は360°ということになります。

　また、何角形であっても棒は必ず最初の位置に戻ってくるので、どんな多角形でも外角の和は360°ということが直感的にわかるかと思います。

正多角形

正多角形とは

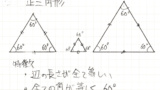
　最後に正多角形です。正多角形とは辺の長さが全て同じとなる多角形です。正三角形については以前こちらで学習しました。

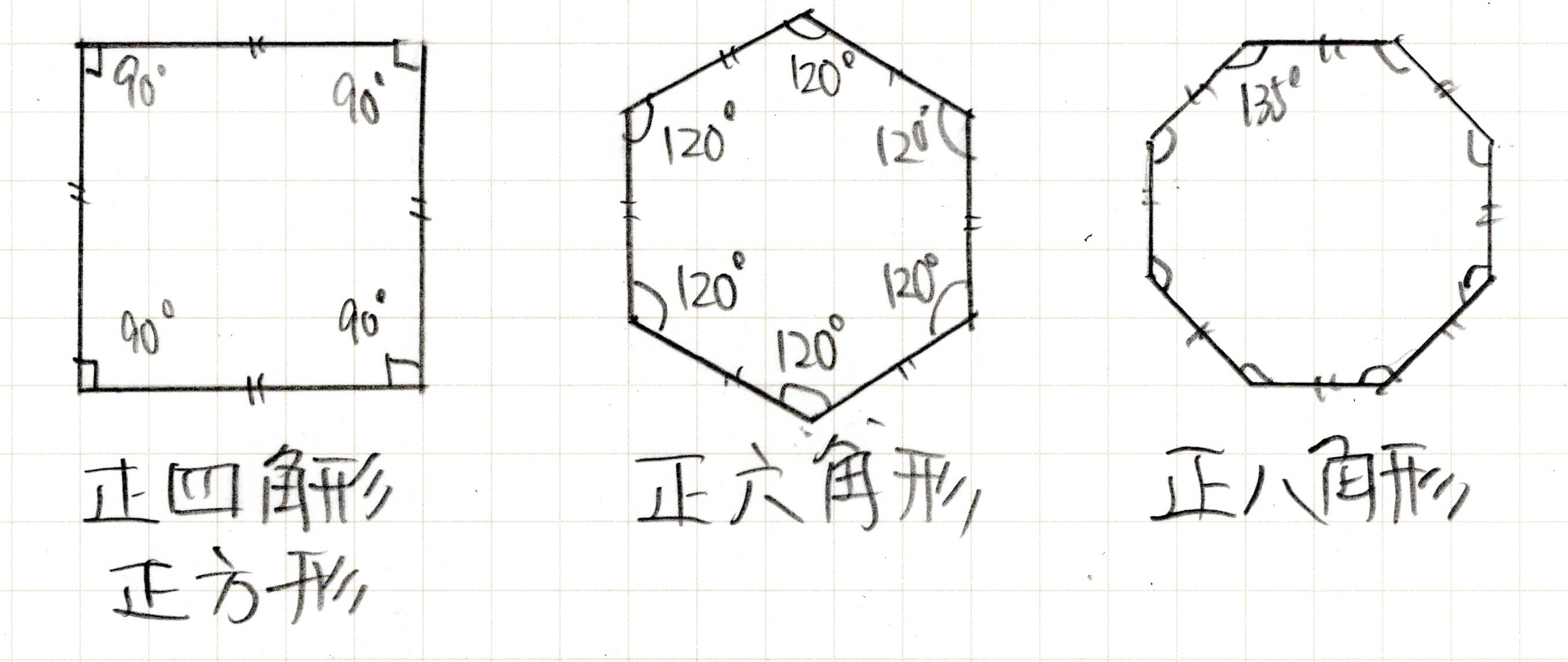
　これの多角形版だと思えばいいです。いくつか正多角形を描いてみます。

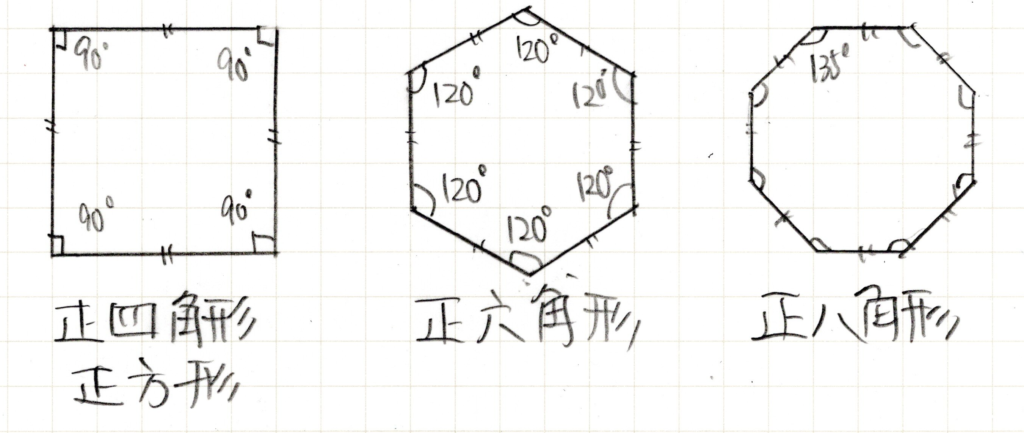
正多角形の特徴

　正多角形の特徴は二つです。

• 全ての辺の長さが等しい
• 全ての内角の大きさが等しい　すなわち　全ての外角の大きさも等しい

　内角の大きさが等しいということは外角はその外側の角なので、外角＝180°ー内角ということから外角も全て大きさが等しくなります。上記二つの特徴を確実に覚えておけばOKです。

問題１

問題

　内角の和は三角形がいくつあるかで探すのでした。

解答

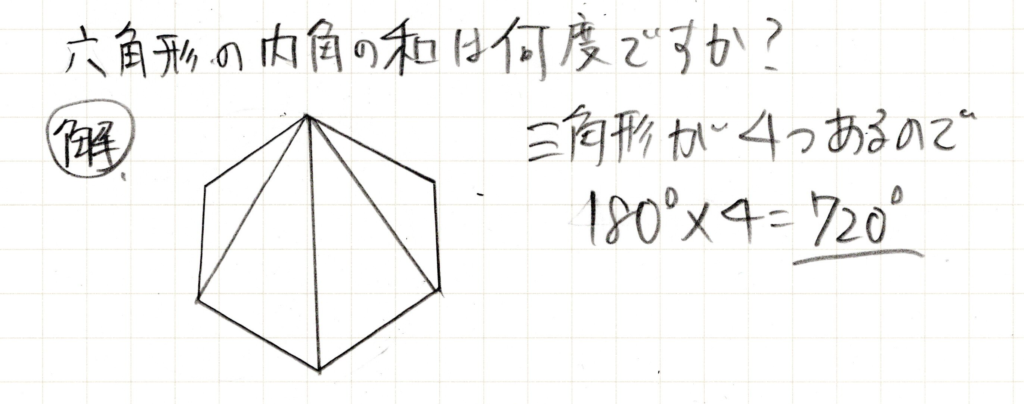
　４つ三角形があることを見つけましょう。

問題２

問題

　三角形から内角の和を求めて順番に探していきます。角が一つ増えると内角の和は180°増えることに気づくとよいです。

解答

　1080°は八角形です。間違っても「1080°÷180°＝6　なので六角形」としないようにしましょう。

問題３

問題

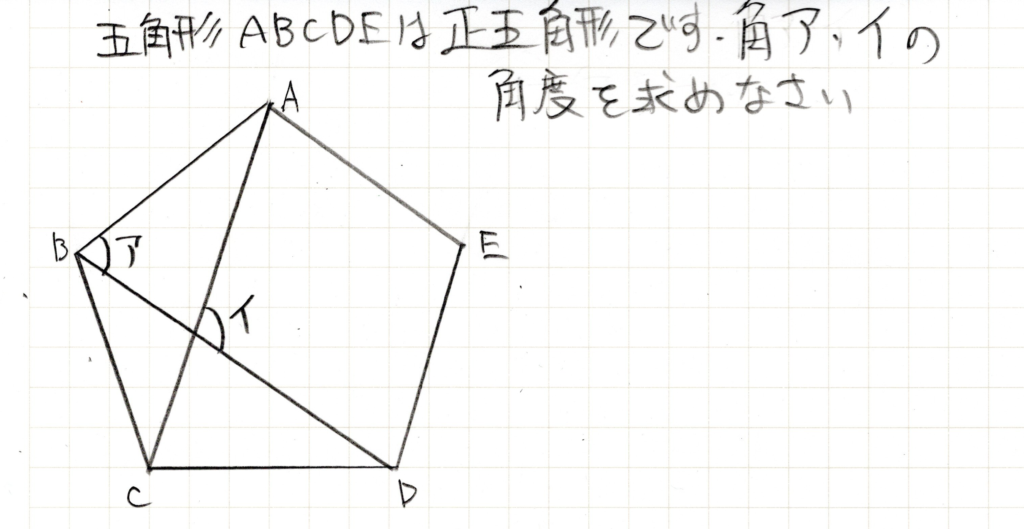
　正多角形の特徴や、外角の求め方などここで学習した知識を総動員します。また、知っているなじみの図形が隠れているのもしっかり探しましょう。二等辺三角形が隠れていないでしょうか・・・？

解答

　正〇角形は全ての内角、全ての外角がそれぞれ等しくなる特徴があります。

　一つの内角を知りたい時、一つの外角を求めて180°から引くというやり方と、内角の和を求めて角数〇で割るという二つのやり方がありますが、ここでは外角から求めるやり方にしました。

　なぜなら、内角の和を求める時、三角形が何個あって・・・と考えると計算ミスなど発生する可能性がありますが、外角は360°を角の数で割れば求まるので、計算ミスしにくいです。

　あと、二等辺三角形がみつかれば角度は求まっていくと思います。二等辺三角形は一つでも角度がわかれば全部わかるというスゴ技を忘れないようにしてください。

　三角形の外角は常に使えるように訓練しておくのも大事なので、あえて最後で使っています。

まとめ

　今回はごちゃごちゃと色々な形が出てきて混乱したかもしれません。大事なことを最後にまとめておきます。

　です。この本質をまずは覚えるようにしましょう。

　前回の記事はこちらから。

　次の記事はこちら。