最初のテーマは数の問題です。数の和、差の基本的なところを学んでいきます。
この記事はうちの子が３年生で学習した算数を振り返り、解説を備忘録的にまとめておこうというシリーズ。教え方は学校の先生、塾の先生、親など教える人それぞれだと思いますので、参考程度にみていただければと思います。
中学受験 は算数がキモといっても過言ではありません。論理的思考はどの教科を学ぶにおいても重要となる、鍛えておくべき力だと個人的には思っています。
問題・解答はPCで作図するより手書きが一番早いので、手書きでまとめています。少々見辛い箇所もあるかと思いますが、ご了承ください。
次の記事はこちら。
和・差
最初は算数の基礎となる和・差についてです。和は足し算の結果、差は引き算の結果です。そして、数の比較を表すのに便利な線分図についても問題でまとめます。
さらに、和・差を理解すればいわゆるつるかめ算も解けてしまうことも説明します。
問題１ 和・差から数を求める その１
問題
解答
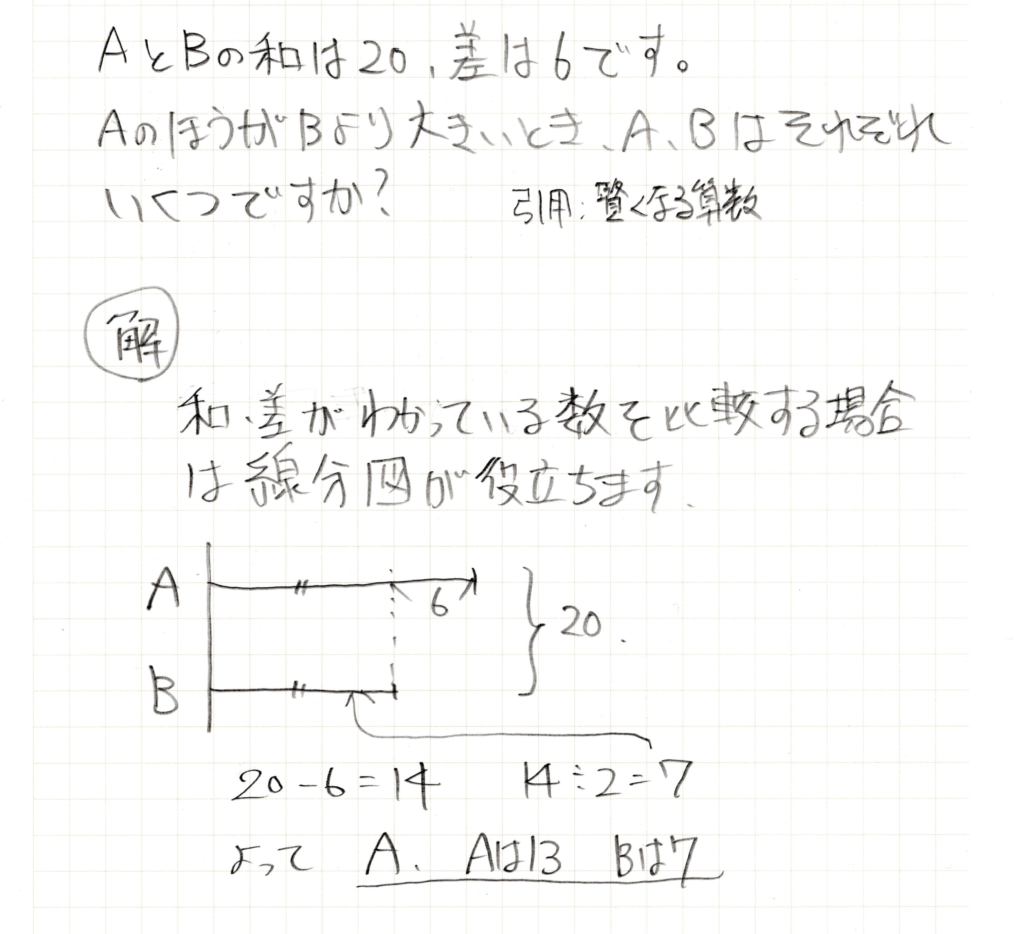
和・差で数を比較する時は線分図が役立ちます。ただ、数字が小さく、低学年の段階では実際にA,Bに数を入れて数を探してみるのがよいと思います。低学年は泥臭く数字を書き出したり、しらみつぶしに探したりする工程が大事になります。
低学年の内に、実際に、書き出して、数えて、泥臭く、苦労して、問題を解いた経験を持っておくと、「こうやって解くと簡単だよ、やりやすいよ、こんなやり方があるよ」という説明が何倍にも重く、しみいるものになると考えています。
問題２ 和・差から数を求める その２
問題
解答
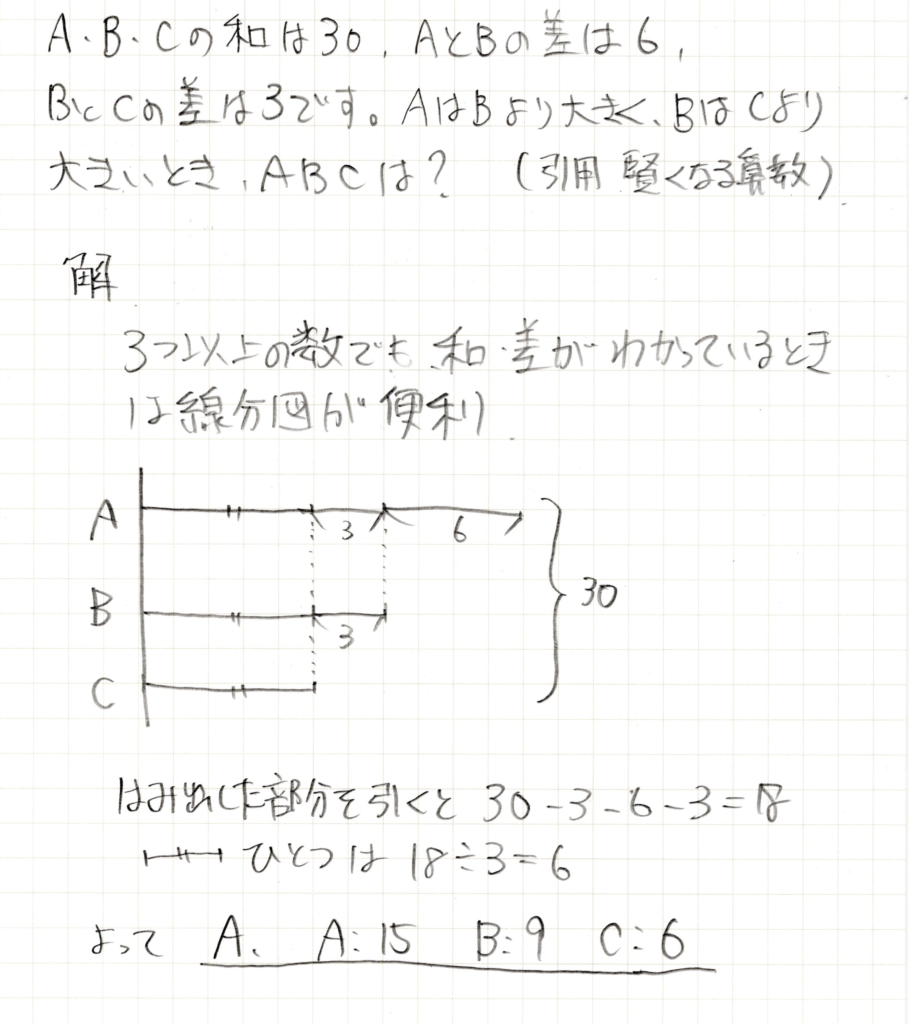
線分図を使った解答はスマートですが、ひとつずつ数を探していくやり方も大事です。この問題を適当に数字を入れて求める場合、何を最初に決定すれば効率よく求められるか？というのに気づくのが特に大事になります。
Aを適当に８とか決めてやってしまうと、Cは０より小さくなってしまいます。なので、Cを適当に決めてB、Aを見つける方法がよいのですが、そこに気づくことは自然と論理的思考の成長につながります。
低学年のうちは、「これは線分図で！」とやり方をこじつけてやらせるより、どうやって答えを探していくか、その過程をしっかり考えさせることが問題の正解を得ることよりも大切だと考えます。
問題３ つるかめ算？？
問題
いわゆるつるかめ算ですね。足が２本、４本のつるかめがいて足の合計が何本でというやつです。和・差を理解しただけのところでいきなりつるかめ算を解くのは厳しい！教え方もわからない！という方もいるかもしれませんが、泥臭くやればいいいんです。低学年ですから。
解答
解１は泥臭いやり方です。数字が小さい問題はこれでいいです。ポイントはいくつかあって、まずA,Bどちらを先に決めるか。そしてA,Bをどのあたりに置いてみるか？
合計が76円なので、Bは15個ほど買えます。もちろんそれにAを買ってしまうと76円をオーバーするのですが、逆に言うとBは15個を超えることはないので、B15個から始めて、14,13と下げていけばいつか答えに当たるはずです。
逆にAから始めると、76円でAは38個買えてしまうのですが、A38個から始めるのは無駄が多そうですよね。
このように泥臭く数えるにしてもどこから数えれば答えに効率よくたどり着けるか？この辺りの感覚を養うことが非常に重要です。
そして解２ですが、いわゆる昔ながらのつるかめ算の解き方に近いやり方ですね。ただ、(100-76)÷3＝8のような計算は使わずに表に書き出しています。
A,Bの増減で合計金額がいくら増減するのかを表にして実際書いてみることが、低学年では重要だと考えます。
おわりに
和、差、線分図の初歩的な範囲ですが、つるかめ算相当の問題も泥臭く解くことができます。昔はつるかめ算と聞くと、難しい！と構えていませんでしたか？少なくとも私は小６でつるかめ算が苦手でよくわかっていませんでした。
しかし、昨今はつるかめ算という言葉も問題集では見なくなりましたし、決まった公式ではなく、きちんと意味を考えて解いたり、泥臭く解いて問題の本質を理解するような時代になったようです。
特に低学年の内は書き出して、手を動かして問題を解くことで論理的思考の感覚を養っていくのが大事かと思いました。
次の記事はこちら。
コメント